Magic Number в лоскутном шитье

«Какое такое Magic Number? Что за магическое число?» Обещаю удивить и порадовать этой маленькой, но очень полезной статьей.

Думаю, вы, как и я, сталкиваетесь с математикой только при расчете лоскутных блоков. Со всем остальным в нашей жизни легко справляется калькулятор, конвертер и пластиковая карта. В смысле даже сдачу пересчитывать не надо.

Иногда нам просто необходимо вычислить длину гипотенузы по длине катетов. Или, по-другому, диагональ квадрата по его сторонам. Так, наверно, понятней.

Что ж, решение есть. Коэффициент 1,414. Умные люди стопудово знают, откуда он взялся. Ваш друг-математик точно расскажет об этом в красках. Я же предлагаю не ломать голову, а просто запомнить.

1,414  1,414  1,414  1,414  1,414

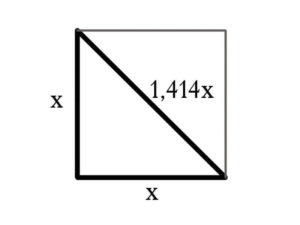
Если сторону квадрата умножить на 1,414, то получится длина диагонали. Или так: если катет равностороннего прямоугольного треугольника умножить на 1,414, то получится длина гипотенузы.

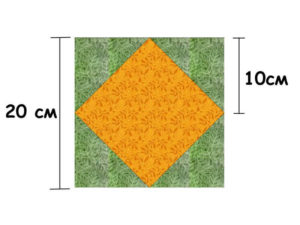
Допустим, сторона нашего квадрата равна 7 см. Значит, его диагональ будет равняться 7 × 1,414 = 9,898 см. Округлим до 9,9 см. Да ладно, можно и до 10 см.

То же будет верно и для дюймов. Сторона квадрата в 3″ даст диагональ = 3″ × 1,414 = 4, 242 или 4″ приблизительно.

Где в лоскутном шитье

пригодится Magic Number

• Для расчета отдельных элементов блока.

Например, мы хотим сшить блок «Квадрат в квадрате». 

Размер блока 20 см. Как узнать параметры внутреннего квадрата? Легко.

Катет углового зеленого треугольника = 20 ÷ 2 = 10 см. Очевидно же. А его гипотенуза, в свою очередь, будет катетом желтого центрального квадрата.

Значит, 10 см × 1,414 = 14,14 см. Или приблизительно 14,2 см.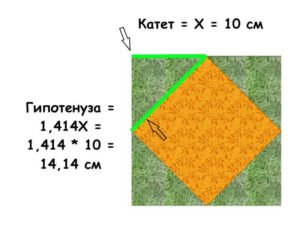Это ширина желтого квадрата. Осталось добавить припуски по 0,75 см.

14,2 +1,5 = 15,7 см в крое.

• Для расчета блоков, поставленных на угол.

Допустим, мы хотим сшить вот такой квилт, скажем, размером 60 на 60 см.

60 см – сумма диагоналей квадратов центрального ряда. Значит, диагональ одного квадрата = 60 ÷ 3 = 20 см.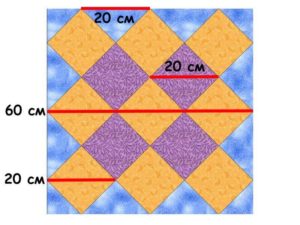

Тогда сторона этого квадрата будет = 20 ÷ 1,414 = 14,1 см.

Плюсуем припуски 14,1 + 1,5 = 15,6 см.  Бинго! Можно кроить.

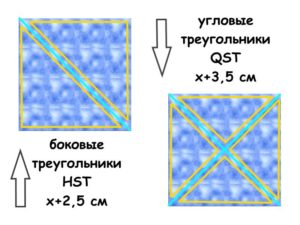
• Также можно рассчитать размеры боковых и угловых треугольников.

Для этого к ширине квадрата 14,1 см добавим другие припуски.

Боковые треугольники изготовим из квадрата, разрезанного пополам. К 14,1 см добавим припуск 2,5 см = 16,6 см.

Угловые треугольники извлечем из квадрата, рассеченного на 4 части по диагоналям. К 14,1 см добавим величину 3,5 см = 17,6 см.

Такие же манипуляции можно произвести и с дюймовыми расчетами.

Я обсчитала много разных вариантов, перепроверяла их на практике с линейкой и так и эдак.  Все работает безупречно!

Думаю, вы тоже по достоинству оцените эту полезную опцию – Magic Number. Я неспроста употребляю только английское название. Ведь в русской лоскутной лексике этого термина нет, потому что даже не все знают о «магическом числе». Но согласитесь, такие знания достойны известности и популяризации.

Особо пытливым умам предлагаю ознакомиться с англоязычной статьей, которая, возможно, добавит вам больше информации.

Пользуйтесь магическим числом, и да пребудет с вами сила, пэчворк-джедаи!